Luna llena sobre Navacerrada

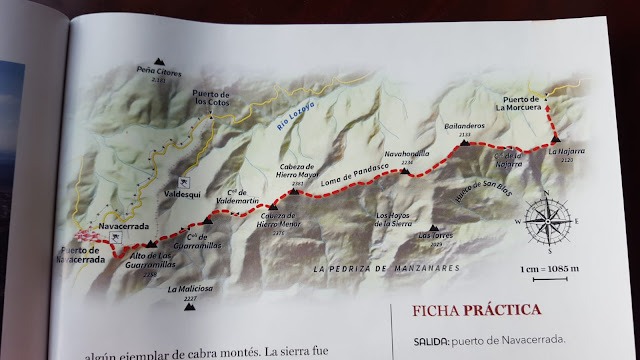
Casi, casi llena estaba la luna este sábado, y bajo su intensa luz plateada nos lanzamos seis caminantes a acometer la Cuerda Larga. Es tradición, ¿quién lo sabía?, en los plenilunios estivales, recorrer la cresta que separa Navacerrada de Morcuera, el espinazo de la sierra entre Madrid y Segovia.

De la hora bruja a la hora del gallo recorrimos las catorce millas entrambos puertos, de la Bola del Mundo al pico Najarra, entre vacas y cabras montesas, al auspicio de Júpiter y Antares, que acompañaban a Selene como dos rémoras de oro. La ruta es difícil, no por la oscuridad, que sí, no por la extensión, que también, y no por el desnivel, que por supuesto, sino por transcurrir entre granito fragmentado, como si se hubiese roto en pedazos la roca de Sísifo y se hubiese desparramado desde la cima.

Tampoco faltó el frío ni nos puso reparos el viento, y se diría que era invierno, y apretamos el paso para cobijarnos al abrigo de la penúltima cumbre, ya tan cerca de la meta, cuando el horizonte se sonrojaba por la parte de Alcalá. Y entre bastiones de cuarzo y feldespato vimos salir a Faetón al galope, riendo exultante como nosotros.

La sierra se tiñó de trinos de pájaros y se roció de colores, desperezándose. A Najarra lo dejamos a nuestra derecha y bajamos por un camino más amable, entre cabras montesas y vacas, al auspicio de Venus Afrodita.

Atmósfera Estándar Internacional (función de Matlab)

He escrito una función para calcular parámetros de la atmósfera en función de la altitud, y aquí la comparto para quien la quiera:

function [T, P, rho, a, mu] = atmosfera(altitud,varargin)
% ATMOSFERA - Datos de la atmósfera estándar internacional.
% La aceleración de la gravedad se supone constante hasta la mesosfera.
% Sintaxis: [T, P, ~] = atmósfera(1000, 'C', 'Pa', 'T_SL', 20)
%
% Entradas: altitud - altitud, en metros, a la que se quiere calcular. La
%           altitud debe ser inferior a 71000 m.
%           T_units - unidad de temperatura para el resultado. Acepta las
%           siguientes: 'K' (kelvin, por defecto), 'C' o 'ºC' (grados
%           Celsius), 'F' o 'ºF' (grados Fahrenheit). Case sensitive.
%           P_units - unidad de presión para el resultado. Acepta las
%           siguientes: 'Pa' (pascales, por defecto), 'atm' (atmósferas),
%           'bar', 'mbar', 'mmHg'. Case sensitive.
%           T_SL (siempre en kelvin) - temperatura a nivel del mar, en caso
%           de que sea diferente de la del día estándar.
%
% Salidas:  T - temperatura a la altitud deseada
%           P - presión a la altitud deseada
%           rho - densidad del aire a esa altitud
%           a - velocidad del sonido a esa altitud
%           mu - viscosidad dinámica del aire a esa altitud
%
% Ejemplos:
%
% Funciones usadas: convertT
%
% Control de cambios ------------------------------------------------------
% Fecha     Autor           Razón
% 14/06/19  Enzo Garabatos  Creado
%
%--------------------------------------------------------------------------

    T_0 = 288.15;  % [K] Temperatura al nivel del mar en día estándar
    P_0 = 101325;  % [Pa] Presión al nivel del mar en día estándar
    g = 9.81;       % [m/s2] Aceleración de la gravedad a nivel del mar
    R = 287;        % [J/(kg·K)] Constante universal del aire
    L = 0.0065;     % [K/m] Tasa de descenso de la T con la altura
    gamma = 1.4;    % [-] Cociente de calores específicos del aire


% -------------------------------------------------------------------------
% input parser siguiendo la recomendación oficial de Mathworks
% //es.mathworks.com/help/matlab/matlab_prog/parse-function-inputs.html
    p = inputParser;
    default_unitsT = 'K';
    valid_unitsT   = {'K', 'C', 'ºC', 'F','ºF'};
    check_unitsT   = @(x)any(validatestring(x,valid_unitsT));
    default_unitsP = 'Pa';
    valid_unitsP   = {'Pa', 'atm', 'bar', 'mbar', 'mmHg'};
    check_unitsP   = @(x)any(validatestring(x,valid_unitsP));

    addRequired(p,'altitude',@isnumeric)
    addOptional(p,'T_units', default_unitsT, check_unitsT)
    addOptional(p,'P_units', default_unitsP, check_unitsP)
    addParameter(p, 'T_SL', T_0, @isnumeric)

    p.KeepUnmatched = true;
    parse(p,altitud,varargin{:})

    T_SL = p.Results.T_SL;

% -------------------------------------------------------------------------
    if altitud < 11000 % Troposfera
        T = T_SL - L * altitud;
    elseif altitud < 20000 % Tropopausa
        T = T_SL - L * 11000;
    elseif altitud < 32000 % Estratosfera inferior
        T = T_SL - L * 11000 + 0.001 * (altitud - 20000);
    elseif altitud < 47000 % Estratosfera superior
        T = T_SL - L * 11000 + 1 * 12 + 0.0028 * (altitud - 32000);
    elseif altitud < 51000 % Estratopausa
        T = T_SL - L * 11000 + 1 * 12 + 2.8 * 15;
    elseif altitud < 71000 % Mesosfera inferior
        T = T_SL - L * 11000 + 1 * 12 + 2.8 * 15 - 0.0028 * (altitud - 51000);
    else
        disp('La altitud excede los límites de esta función')
        return
    end
   
    P   = P_0 * (T/T_SL)^(g/L/R);
    rho = P / (R * T); % de la ecuación de estado de los gases
    a = (gamma * R * T) ^ 0.5; % [m/s]
    mu = 0.1456e-5 * (T)^0.5 / (1 + 110/T); %[Pa·s] viscosidad dinámica

% Conversión de los resultados a las unidades requeridas por el usuario ---
    T = convertT(T,'K',p.Results.T_units);

    switch p.Results.P_units
        case 'atm'
            P = P /101325;
        case 'bar'
            P = P/1e5;
        case 'mbar'
            P = P/100;
        case 'mmHg'
            P = P * 760 / 101325;
    end
% -------------------------------------------------------------------------

end

Utiliza la siguiente función para cambiar entre unidades de temperatura:

function T = convertT(T, unit,new_unit)
    switch unit
        case 'K'
            switch new_unit
                case {'C', 'ºC'}
                    T = T - 273.15;
                case {'F', 'ºF'}
                    T = (T + 273.15) * 1.8 + 32;
            end
        case {'F', 'ºF'}
            switch new_unit
                    case {'C', 'ºC'}
                    T = (T - 32)/1.8;
                case 'K'
                    T = (T - 32)/1.8 - 273.15; 
            end
        case {'C', 'ºC'}
            switch new_unit
                case {'F', 'ºF'}
                    T  = T * 1.8 + 32;
                case 'K'
                    T = T + 273.15;
            end
    end
end

Cualquier comentario o sugerencia es bienvenida.